Hat man eine Menge von Testpunkten die man mit einer geraden Linie approximieren will so hat man mehrere Möglichkeiten. In Python ist es am einfachsten, die Daten in ein Array einzugeben und damit die Funktion lingress() aus dem scipy.stats-Paket aufzurufen. Dadurch bekommt man immerhin neben der Steigung und dem Offset der Regressionsgeraden auch noch die Statistik-Werte p und r geschenkt. Doch was für Mathematiker, wenn nicht selbst wagen…
Die Methode der kleinsten Quadrate
Man kann die Aufgabe umformulieren: Gesucht sind a_{0} und a_{1} so, dass die Summe aller Distanzen der Messpunkte zu den entsprechenden Punkten auf der Gerade y = a_{0}x^0 + a_{1}x^1 so klein wie möglich wird. Wenn man diese Gerade unter Verwendung dieser Distanzen sucht, hat man die Methode der kleinsten Quadrate eingesetzt. Es gibt einige Erläuterungen im Internet über dieses Verfahren. Die kürzeste Schreibeweise der ausformulierten, analytischen Closed Form mit der a_{1} berechnet werden kann ist:
a_{1}=\frac{\sum\limits_{i=1}^{n}(x_{i}y_{i}) - n\tilde{x}\tilde{y}}{(\sum\limits_{i=1}^{n}x_{i}^{2})-n\tilde{x}^{2}}
Dabei sind \tilde{x} und \tilde{y} sind die Durchschnitte aller Messpunkte.
Um a_{0} auszurechnen muss man das eben berechnete a_{1} in folgende Formel für a_{0} einsetzen und umformen:
na_{0} + (\sum\limits_{i=1}^{n})a_{1} = \sum\limits_{i=1}^ny_{i}
Ja und viel Spaß dabei! Aktuelle Problemstellungen können mehrere Millionen Messpunkte enthalten. Die notwendigen Berechnungen in dieser expliziten Methode sind nichts für ungeduldige.
Gradientenabstiegsverfahren
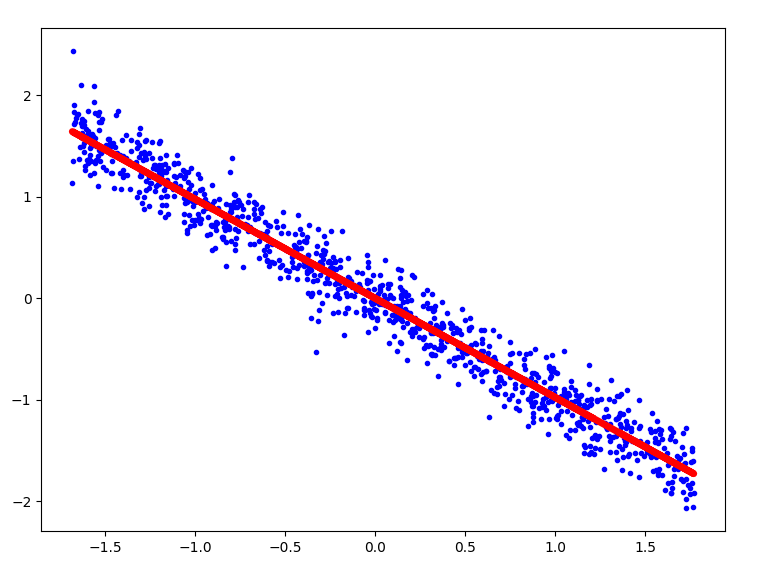
An dieser Stelle kann uns das Gradientenabstiegsverfahren helfen. Gretchenhaft gesagt^{(1)}, zeichnet man mit beliebig geschätzen Startwerten für a_{0} und a_{1} die Gerade in die Messpunkte ein, berechnet den Gradienten (die Ableitung) einer sogenannten Fehler-Funktion^{(2)}. Dann verändert man die Steigung der Geraden um einen Bruchteil ^{(3)} entgegengesetzt zum Gradienten der Fehlerfunktion, damit die nächste Hypothese \hat{y} näher an y liegt.
Mathematisch anschaulich sieht die Fehlerfunktion so aus:
MSE=\frac{1}{2n}\sum\limits_{i}(\hat{y}_{i}-y_{i})^{2}=\frac{1}{2n}\sum\limits_{i}(w^{T}x_{i}-y_{i})^2Und die Ableitung davon nach \frac{\partial}{\partial{x}}:
\frac{\partial}{\partial{w_{j}}}MSE = \frac{1}{n}(w_{j}x_{i} - y_{i})x_{ij}Uff, wer bis hier noch dabei ist hat es geschafft. Falls nicht – macht nichts – vielleicht hilft ein Blick in den Code.
^{(1)} Ja, es ist gretchenhaft, denn mäxchenhaft ist ja lächerlich. ^{(2)} Eine Fehlerfunktion ist abhängig von einem X und liefert einen Fehler. Das gute an dieser Darstellung ist, dass man die Funktion ableiten kann und dadurch einen Fehler-Gradienten erhält, der wiederum hilft die ursprüngliche Hypothese (Regressionsgerade) zu verbessern. ^{(3)} Diesen Bruchteil nennt man für gewöhnlich Lernrate. Der Buchstabe dazu ist \eta (sprich: eta)
import numpy as np
import matplotlib.pyplot as plt;
X = 5 * np.random.rand(1000, 1)
y = (np.random.rand()*10-5) + (np.random.rand()*10-5)*X + np.random.randn(1000, 1)
class LinearRegressionGD():
def __init__(self, η = 0.0001, epochen = 50):
self.η = η # Lernrate
self.epochen = Epochen
def fit(self, X, y):
# gesucht ist ein w so dass ∀ x ∈ X: ŷ = w[1]∙x + w[0] liegt möglichst nahe an y
self.w = np.zeros(1 + X.shape[1])
for i in range(self.epochen):
ŷ = self.predict(X)
err = y.flatten() - ŷ # Fehler
#mse = (err ** 2).sum() / 2.0 / len(X) # aufsammeln und ausgeben, wird in Rechnung nicht gebraucht
self.w[1:] += self.η * X.T.dot(err) # Anpassen des Gewichts Beta (und falls es sie gäbe: aller weiteren Gewichte)
self.w[0] += self.η * err.sum() # Anpassen des Gewichts Alpha
return self
def predict(self, X):
return np.dot(X, self.w[1:]) + self.w[0] # y = x * Beta + Alpha
x_std = X
y_std = y
# Zum Probieren mit μ=0 und σ=1
#x_std = (X - X.mean()) / X.std()
#y_std = (y - y.mean()) / y.std()
lrGD = LinearRegressionGD() # Instanz erzeugen
lrGD.fit(x_std, y_std)
plt.figure(figsize = (15, 15))
plt.plot(x_std, y_std, "b.") # Scatter
plt.plot(x_std, lrGD.predict(x_std), "r-", linewidth = 5) # Regressionsgerade als Linie
plt.show()
Alternative Implementierung
Nicht ganz so effizient, aber doch lehrreich ist die nächste Implementierung. (In Wirklichkeit war das mein erster Versuch :-))
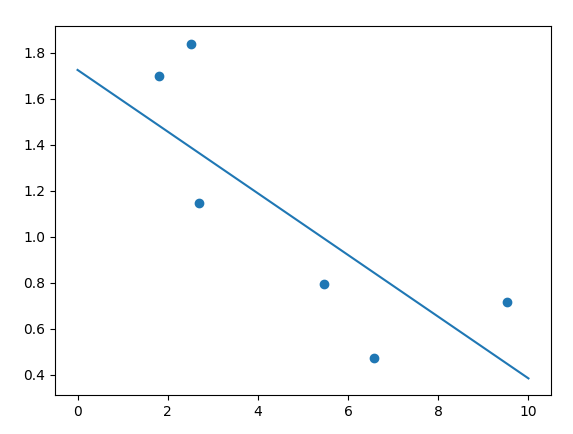
Es werden insgesamt viel weniger Punkte mit mehr Rechenaufwand approximiert. Aber ohne die Matrizen-Tricks wie beim Verfahren oben, kann man viel besser zusehen, wie die Regressionsgerade langsam zum Optimum hingedreht wird.
import numpy as np
import matplotlib.pyplot as plt
# Definiere n Punkte (x, y) ∈ ([0, maxx], [0, maxy])
n = 6
maxx = 10
maxy = 2
x = np.random.rand(n)*maxx
y = np.random.rand(n)*maxy
# Plot der n Punkte
plt.scatter(x, y)
η = 0.001 # lernrate
m = 0.0 # Zufällige Steigung
b = 0.0 # Zufälliger Offset
ϝ = lambda x: m*x + b # f(x) = mx + b
print("---------------------")
previous_sdm = 123
j = 0
for j in range(2000):
cost = 0.
sdm = 0.
sdb = 0.
# gehe alle Punkte durch und summiere die Fehlerquadrate
for i in range(len(x)):
δ = y[i]-ϝ(x[i]) # δ ist der Unterschied zwischen der Vorhersage und dem i-ten Messwert
loss = δ**2 # loss ist das Quadrat
db = -δ # Ableitung der cost-Funktion nach b
dm = -δ * x[i] # Ableitung der cost-Funktion nach m
cost = cost + loss
sdm = sdm + dm
sdb = sdb + db
m = m - η * sdm # korrigiere m in entgegengesetzer Richtung der Steigung (downhill)
b = b - η * sdb # dito mit b
# Vielleicht haben wir ja ein ausreichend gutes Ergebnis
if np.abs(previous_sdm - sdm) < 0.00000001:
print("end after {} steps".format(j))
break
previous_sdm = sdm
#print(sdm)
print("Total cost: {:.3f}, {:.3f}, {:.3f} in {} steps".format(cost, sdm, sdb, j))
p = np.linspace(0, maxx, 2) # wir brauchen nur 2 Punkte für die Gerade
plt.plot(p, ϝ(p))
plt.show()