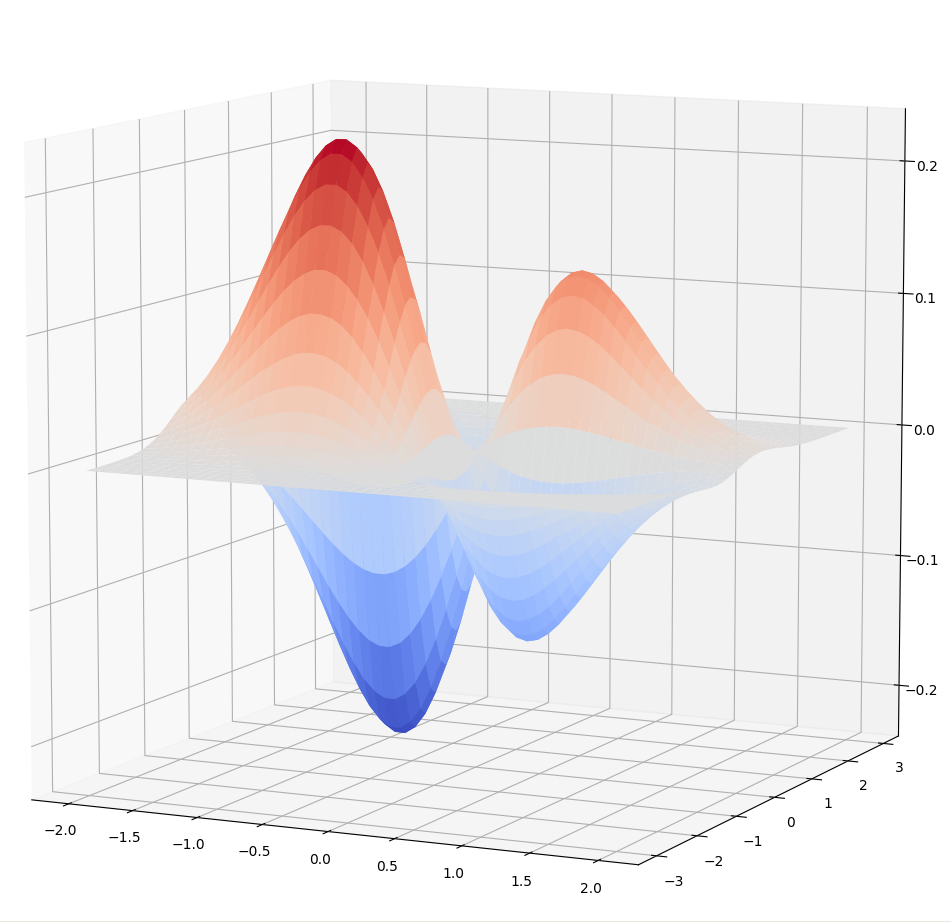
Hier wird ein Problem des Gradientenverfahrens anhand einer Funktion mit zwei Buckeln und zwei Tälern (4 Extremwerte) untersucht.
(x,y) → (x∙sin(y))∙exp(-x²-y² -0.4x)
Die Funktion ist stetig, beschränkt und nicht symmetrisch. Deshalb gibt es mehrere lokale und globale Extremwerte.
Das Gradientenverfahren findet Minima, doch je nach Wahl des Startpunktes für den Algorithmus, landet es entweder in einem lokalen oder im globalen Minimum.
Beim Start in (-1.0, 1.0) kommt man zum globalen Minimum -0.23 bei (-0.81, -0.23)
und beim beim Start in (0.5, -0.5) kommt man zum lokalen Minimum -0.13 bei (0.61, -0.65)
Der Code zeigt eine Implementierung einfache Implementiertung. Zur Verifikation wird das Minimum auch noch mit Scipy berechnet.
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fmin_tnc
# Funktion, deren Minimum gesucht wird
def f(x):
return (x[0]*np.sin(x[1]))*np.exp(-x[0]**2 -0.4*x[0] -x[1]**2)
# Hilfsroutine um Distanz zwischen zwei Punkten.
# Fuer das Abbruch-Kriterium in der eigenen Implementierung
def distance(a, b):
return np.sqrt((a[1]-b[1])**2+(a[0]-b[0])**2)
# Plot-Fenster soll mit ESC schliessen
def close_on_escape(figure):
def press_key(event):
if event.key == 'escape':
plt.close('all')
elif event.key == 'q':
exit()
figure.canvas.mpl_connect('key_press_event', press_key)
# Plot-Fenster von -3 bis 3 auf beiden Achsen
def draw( function ):
fig = plt.figure(figsize=(15,15))
close_on_escape(fig)
ax = fig.gca(projection='3d')
X = np.linspace(-3, 3, 50)
Y = np.linspace(-3, 3, 50)
X, Y = np.meshgrid(X, Y)
Z = function([X, Y])
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
# Klassische Gradienten-Berechnung ohen jegliche Optimierung oder Pruefung
def grad(f, a, b):
ε = 0.00001
y = f([a, b])
dx = (f([a+ε,b]) - y)/ε;
dy = (f([a,b+ε]) - y)/ε;
return [dx, dy];
if __name__ == "__main__":
#x = 0.5; y = -0.5 # Findet lokales Minimum
x = -1.0; y = 1.0 # Findet globales Minimum
# Scipy rechnen lassen
ergebnis = fmin_tnc(f, [x, y], disp=False, approx_grad=True, bounds=[(-3,3), (-3,3)])
z = f([ergebnis[0][0], ergebnis[0][1]])
print(f"Minimum: {z:.3f} bei ({ergebnis[0][0]:.3f}, {ergebnis[0][1]:.3f}) - scipy")
# Selbst rechnen
previous_g = [0, 0]
for step in range(10000):
current_g = grad(f, x, y)
x -= current_g[0]
y -= current_g[1]
if distance(previous_g, current_g) < 0.001:
break
previous_g = current_g
print(f"Minimum: {f([x,y]):.3f} bei ({x:.3f}, {y:.3f}) - selbst gerechnet")
draw(f)