Im folgenden wird es um Q-Learning gehen.
Dabei ist q eine Art Mass für die Qualität einer Aktion hinsichtlich der daraufhin zu erwartenden, zukünftigen Belohnungen.
Hohe q-Werte entsprechen hohen Belohnungen und ein Agent der sich in einem Spiel befindet ist bestrebt die Belohnung zu maximieren.
Die zentrale Komponente im Q-Learning ist die Q-Tabelle. Das ist eine Matrix, bestehend aus Zeilen, die mit Systemzuständen assoziiert sind und aus Spalten die den einzelnen Aktionen entsprechen die ein Agent in einem entsprechenden Zustand ausführen kann.
| q(Status 1, Aktion 1) | q(Status 1, Aktion 2) | … | q(Status 1, Aktion M) |
| q(Status 2, Aktion 1) | q(Status 2, Aktion 2) | … | q(Status 2, Aktion M) |
| … | … | … | … |
| q(Status N, Aktion 1) | q(Status N, Aktion 2) | … | q(Status N, Aktion M) |
Im Training wird die Q-Tabelle durch folgenden Algorithmus aufgebaut:
Setze Parameter:
α ∈ (0, 1] - Lernrate - ca 0.2
γ ∈ )0, 1( - Gewichtung zukünftiger Ereignisse - ca 0.95
ε > 0 - Explore/Exploit-Ratio, ca 0.10
Initialisiere alle Q(s,a) = 0
Loop Episoden (Spiele):
Reset S
While S != Terminal
Ermittle die im Zustand S möglichen Aktionen
Wähle eine der Aktionen mithilfe der durch Q induzierten Policy
Führe die gewählte Aktion und ein Update der Q-Tabelle durch:
Update Q(S,A) = (1-α)*Q[S,A] + α*(R[S,A]+γargmax(Q[S',a])
Übernehme den neuen Zustand: S = S'
Das war’s auch schon mit der Theorie. Es gibt zwar noch einige Varianten wie z.B. ein mit der Zeit abnehmendes Epsilon, um Anfangs wegen einem besseren Explore/Exploit-Verhältnis schneller zu einer besseren Policy zu gelangen, doch die Vor- bzw. Nachteile die das System mit sich bringt werden durch solche Variationen nicht wesentlich verändert.
Bevor wir jetzt tiefer in ein Beispiel eintauchen laden wir vorab in einer Python-Shell oder in einem jupiter notebook schon mal die Standard-Module.
import numpy as np
import pylab as plt
import networkx as nx
import random
#from IPython.core.debugger import set_trace
Für das folgende Beispiel stelle man sich ein Haus mit N Zimmern vor und wie man in einem dieser Zimmer aufwacht.
Wir haben initial keine Ahnung wie wir aus dem Haus herauskommen können.
Zwar gibt es einen Netzplan der Zimmer, doch aufgrund der überwältigenden Anzahl der Zimmer sehen wir den Weg zum Ausgang (Raum 110) nicht.
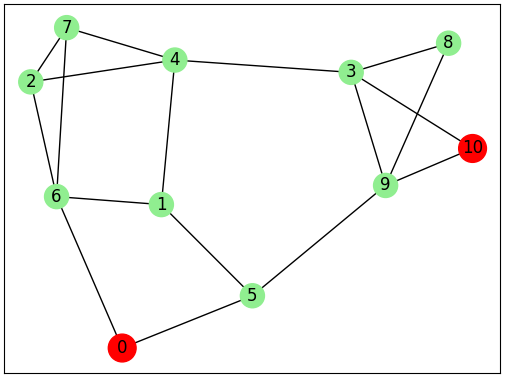
Um diese Situation zu modellieren, nummerieren wir die Zimmer von 0 bis N-1 und beschreiben eine Verbindung als 2-Tupel mit den beiden Zimmern die durch einen Korridor oder eine Türe verbunden sind.
Als erstes definieren wir eine Funkion die eine Liste mit Verbindungen zwischen Räumen erstellt
def build_rooms(N):
connections = []
for r in range(2): # Es gibt zwei Wege von Raum 0 zum Raum N
route = [i for i in range(1, N-1)]
np.random.shuffle(route)
for i in range(r):
route.pop()
route.append(0)
route = route[::-1]
route.append(N-1)
for j in range(len(route)-1):
connection = (route[j], route[j+1])
connections.append(connection) # [ (1,2), (2,3), (3,4), ...]
return connections
Dann brauchen wir noch eine Hilfsfunktion um den Netzplan anzuzeigen:
def show_net(net):
G=nx.Graph()
G.add_edges_from(net)
color_map = []
size_map = []
for i in range(N):
if i == 0 or i == N-1:
color_map.append('red')
size_map.append(400)
else:
color_map.append('lightgreen')
size_map.append(300)
pos = nx.spring_layout(G)
nx.draw_networkx_nodes(G, pos, node_color=color_map, node_size=size_map)
nx.draw_networkx_edges(G, pos)
nx.draw_networkx_labels(G,pos)
plt.show()
Aus den Verbindungsdaten kann eine Reward-Matrix erstellt werden. Dort wo keine Verbindung zwischen zwei Räumen existiert, steht in der Reward-Matrix eine -1.
Die Verbindungen zum Zielraum werden mit 100 belegt. Allen anderen Verbindungen enthalten eine 0.
def generate_rewards_matrix(N, connections):
R = np.matrix(np.ones(shape=(N, N)))
R*=-1
for connection in connections:
if connection[1] == N-1:
R[connection] = 100
else:
R[connection] = 0
R[connection[::-1]] = 0
R[N-1,N-1] = 100
return R
Die Funktion die den nächsten Spielzug auswählt hat den Parameter ε mit dem die Greedy-Rate gesteuert wird. Im Wettkampf wird er auf 1 gesetzt und im normalen Training auf einen kleinen Wert > 0.
def select_action(S, epsilon=0):
available_actions = np.where(R[S,] >= 0)[1]
if np.random.rand() < epsilon:
# Explore
return int(np.random.choice(available_actions, 1))
# Exploid
allq = [Q[S, index] for index in available_actions]
action = np.random.choice(np.where(allq == max(allq))[0], 1)
return int(available_actions[action])
Das einzige was jetzt noch fehlt ist das Update der Q-Matrix:
def update(S, A, gamma):
alpha=0.1
next_actions = np.where(R[A,] >= 0)[1]
v = [Q[A, index] for index in next_actions]
maxa = int(np.random.choice(np.where(v == max(v))[0], 1))
Q[S,A] = Q[S,A] + alpha * (R[S,A] + gamma*v[maxa] - Q[S,A])
if(np.max(Q) > 0):
return (np.sum(Q/np.max(Q)*100))
else:
return (0)
Jetzt kann das System trainiert werden
def train():
gamma=0.90
previous_score = 0
scores = []
epochs = 1000 # es werden 1000 Spiele gespielt
for i in range(epochs):
state = np.random.randint(0, int(Q.shape[0]))
action = select_action(state, epsilon=.5)
score = update(state, action, gamma)
scores.append(score)
#print( score, score - previous_score )
previous_score = score
print(np.round(Q/np.max(Q)*100))
return scores
In einer Test-Loop prüfen wir die gelernten Wege
def test(N):
current_state = 0
steps = [current_state]
for i in range(N-1):
current_state = i
steps = [current_state]
counter = 0
while current_state != N-1:
if counter > 10 :
break
counter += 1
next_step_index = np.where(Q[current_state,] == np.max(Q[current_state,]))[1]
if next_step_index.shape[0] > 1:
next_step_index = int(np.random.choice(next_step_index, size=1))
else:
next_step_index = int(next_step_index)
steps.append(next_step_index)
current_state = next_step_index
print(steps)
Und jetzt müssen wir nur noch die Funktionen aufrufen
N=11
connections = build_rooms(N)
R = generate_rewards_matrix(N, connections)
Q = np.matrix(np.zeros([N, N]))
show_net(connections)
scores=train()
test(N)
test(N)
Und schliesslich die Anzeige des Lernfortschritts
plt.plot(scores)
plt.show()